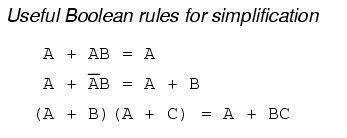Digital Weekly Jurnal#3 :: CONVERTING TRUTH TABLES INTO BOOLEAN EXPRESSIONS

      การออกแบบวงจร Logic นั้น บางที่เราต้องการ Input 3 Input ขึ้นไปนั้น และให้ Output เป็น 1 โดยที่ มี Input เป็น 1 นั้น 2 Input เป็นต้นไป ซึ่งการออกแบบ Truth Tables นั้นในบางกรณี ดังเช่น

            เมื่อเรามาคำนวณ GATE ดังตัวอย่างนี้ เราจำเป็นต้องใช้ GATE จำนวน 3 Input เป็นอย่างต่ำ เพื่อให้ได้ผลลัพท์ตาม Truth Tables ดังกล่าว และในการต่อวงจรนั้น สุดท้ายแล้วเราก็ยังไม่รู้ว่าจะต้แงต่อวงจรยังไงและใช้จำนวน GATE เท่าไร อะไรบ้าง

     ซึ่งคราวนี้จะมาดูว่าเราสามารถกระทำอะไรกับตาราง Truth Table นี้ได้บ้าง

1.) Sum - of - products ( SOP )

     Sum of products คือการทำ Boolean Expression ในรูปของการบวกกันของผลคุณ เช่น ABC+AC+BC 

**เสริม Boolean Expression คือ การแปลงจาก Truth Tables ที่เราสนใจนั้น ให้อยู่ในรูปของสมการ **

กรณีนี้ เราเขียน Boolean Expression ในรูปผลคุณของ Input ใดที่ทำให้ Output เป็น "1"

จากนั้นก็เขียน Boolean Expression ให้อยู่ในรูปของ Sum of products จะได้

      จากนั้น เราก็จะได้ Logic Gates เป็นหน้าตา ดังนี้

ยังไงก็ตามวงจรนี้ก็ยังดูซับซ้อนมากต่อการ implement ดังนี้เราสามารถลดรูปลงได้ โดยใช้เทคนิคของ Boolean Algebra

           Boolean Algebra หรือ พีชคณิตของบูลีน เป็นหลักทางคณิตศาสตร์ที่ใช้วิเคราะห์ปัญหาทางตรรก ถูกคิดค้นโดยนักคณิตศาสตร์ชาวอังกฤษ ชื่อ จอร์จ บูล( George Boole ) ค่อมาก็มีผู้พัฒนาให้สมบูรณ์ขึ้นอีกหลายคน ปัจจุบันนี้เราใช้พีชคณิตของบูลีนในการออกแบบวงจร Logic Gates ซึ่งเป็นการลดความยุ่งยากของวงจรลง

        1.) เอกลักษณ์ของบูลีในการบวก

            1.1 A + 0 = A เพราะว่า ต่อให้ A=0 ผลที่ได้คือ 0 + 0 = 0 และถ้า A = 1 ผลที่ได้คือ  1 + 0 = 1 ดังนั้นจึงสรุปว่า A + 0 = A

            1.2 A + 1 = 1 เพราะว่า ต่อให้ A=0 ผลที่ได้คือ 0 + 1 = 1 และถ้า A = 1 ผลที่ได้คือ  1 + 1 = 1 ดังนั้นจึงสรุปว่า A + 1 = 1

            1.3 A + A = A เพราะว่า เราเอาขา Input มาต่อร่วมกัน เลยทำให้ A=0 ผลที่ได้คือ 0 + 0 = 0 และถ้า A = 1 ผลที่ได้คือ  1 + 1 = 1 ดังนั้นจึงสรุปว่า A + A = A

            1.4 A +`A= 1 เพราะว่า เราเอาขา Input มาต่อร่วมกันและมีขาหนึ่งที่ต่อแบบ Inverts ไว้ เลยทำให้ A=0 ผลที่ได้คือ 0 + 1 = 1 และถ้า A = 1 ผลที่ได้คือ  1 + 0 = 1 ดังนั้นจึงสรุปว่า A +`A= 1

หมายเหตุ `A คือ Inverts ของ A เช่นกัน

      2.) เอกลักษณ์ของบูลีในการคุณ

            2.1 0A = 0 เพราะว่า ต่อให้ A=0 ผลที่ได้คือ 00 = 0 และถ้า A = 1 ผลที่ได้คือ  01 = 0 ดังนั้นจึงสรุปว่า 0A = 0

            2.2 1A = A เพราะว่า ต่อให้ A=0 ผลที่ได้คือ 10 = 0 และถ้า A = 1 ผลที่ได้คือ  11 = 1 ดังนั้นจึงสรุปว่า 1A = A

            2.3 AA = A เพราะว่า เราเอาขา Input มาต่อร่วมกัน เลยทำให้ A=0 ผลที่ได้คือ 00 = 0 และถ้า A = 1 ผลที่ได้คือ  11 = 1 ดังนั้นจึงสรุปว่า AA = A

            2.4 A`A= 0 เพราะว่า เราเอาขา Input มาต่อร่วมกันและมีขาหนึ่งที่ต่อแบบ Inverts ไว้ เลยทำให้ A=0 ผลที่ได้คือ 01 = 0 และถ้า A = 1 ผลที่ได้คือ  10 = 0 ดังนั้นจึงสรุปว่า A`A= 0

หมายเหตุ `A คือ Inverts ของ A เช่นกัน

สรุป เอกลักษณ์ของบูลีนจะเป็นไปตามนี้

*** เพิ่มเติม : ถ้าเราต่อ Inverts 2 ชั้น ผลที่ได้คือ จะได้ผลลัพธ์เหมือน input ทันที

          คุณสมบัติของบูลีน

             1. การสลับที่ (Commutative law)

 A + B = B + A   และ  AB = BA

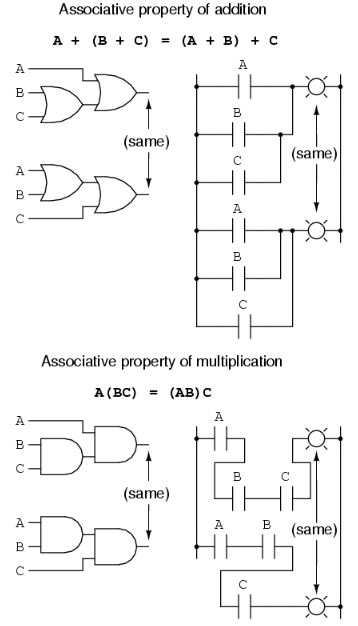
             2. กฎการจัดหมู่ (Associative law)

(A + B)+C = A+(B + C)  และ (AB)C = A(BC)

             3. กฎการกระจาย (Distributive law)

A(B + C) = AB+AC และ A+(BC) = (A+B)(A+C)

สรุป คุณสมบัติของบูลีนเป็นไปตามนี้

           การลดรูปโดยใช้กฎของบูลีน

              1. A + AB = A

                   เกิดจาก...

จะได้รูปวงจรดังนี้

              2. A + `AB = A+B

                   เกิดจาก...

จะได้รูปวงจรดังนี้

หมายเหตุ `A คือ Inverts ของ A เช่นกัน

              3. (A+B)(`A+C) = A + BC  

                   เกิดจาก...

จะได้วงจรดังรูปต่อไปนี้

สรุป การลดรูปโดยใช้กฏของบูลีนจะเป็นดังนี้

หมายเหตุ `A คือ Inverts ของ A เช่นกัน

    เกี่ยวกับ The Exclusive - OR Function (XOR)

                XOR 1 ตัว จะมีลักษณะเหมือนกับ A`B + `AB 

     ลองลดรูปวงจรโดยการใช้กฎของบูลีนกันเถอะ

            จากวงจรนี้ เราสามารถลดรูปวงจรโดยใช้บูลีนได้เป็นดังนี้

         

จะเหลือรูปวงจรเพียงแค่นี้

          อารัมภบทต่อมา เราต้องเพิ่ม Output ขึ้นมาอีก 1 หล่ะ คราวนี้เราจะทำเยี่ยงใย???

            ถ้าเห็นอย่างนี้เราคงทำ SOP อย่างแน่นอนซึ่งผลของ Boolean Expression ก็จะได้แบบนี้

         ซึ่งเราสามารถนำ Boolean Expression นี้ไปลดรูปได้ปกติแต่จะมีโอกาสผิดสูงมากเพราะมีจำนวนพจน์ถึง 6 พจน์ด้วยกัน ซึ่งมากพอสมควร ซึ่งเราจะมาเรียนรูปวิธีลดต่อไปคือ

2.) Products - of - sum ( POS )

       Products of sum  คือการทำ Boolean Expression ในรูปของการคูณกันของผลบวก เช่น (A+B+C)(A+C)(B+C) แต่คราวนี้เราจะสนใจที่ Output เป็น "0"

ซึ่งจะทำให้ได้วงจรเพิ่มเต็มเป็นดังนี้

และเช่นเดียวกันเราสามารถลดรูปวงจรนี้ได้โดยใช้ Boolean Algebra ได้เช่นกัน

       DeMorgan's theorem

     ทฤษฏีที่สำคัญอีกทฤษฎีของ Digital Logic โดยพื้นฐานแล้วมันมีไว้เพื่อแปลงรูปนิเสธของ logic เพื่อช่วยให้ง่ายต่อการคำนวณ Boolean Algebra และบทเด่นของมันคือ ยุบ bar กรณีที่มี 2 bar ขึ้นไปได้

 ตัวอย่างของ DeMorgan ในการแทนอุปกรณ์

 ตัวอย่างการใช้ DeMorgan Law.

  Ref :: http://www.electrical4u.com/de-morgans-theorem-and-demorgans-laws/

***ทิ้งทายด้วย***

ทำไม Sum (บวก) ต้องแทนด้วย OR Gates??

ทำไม Product (คูณ) ต้องแทนด้วย AND Gate??

นั่นก็เพราะ.......ตามนั้นนะ

Class Work

1.) ทำการต่อวงจร SOP ดังตัวอย่างวงจรข้างบน พบว่า สายเยอะมาก และการทดลองเป็นไปด้วยดี

2.) ทำการเพิ่มวงจรในส่วนของ POS ลงไปด้วย ซึ่งได้ลดรูปวงจรจากตัวอย่างแล้วได้เป็น

ทำให้ได้หน้าตาวงจรออกมาเป็นดังนี้

และนี้คือผลของการต่อวงจรจริง

หน้าตาเหมือนข้างบนมากแทบแยกไม่ออก

ซึ่งผลจากการทดลองก็ได้สรุปเป็นวีดีโอเป็นที่เรียบร้อยแล้ว

ปัญหาหลักๆก็คือ

1) เราไม่มี Gate input แบบ 3 ขา ซึ่งผลตรงนี้เราก็สามารถประยุกต์ได้โดยใช้ OR Gates 2 ตัวต่อร่วมกัน                                              

2) ลองพยายมลดรูป POS โดยไม่ใช่ XOR ผลปรากฎว่า เยอะยิ่งกว่าเดิมซะอีก เลยต้องทำใจยอมใช้ XOR

**หมายเหตุ ที่ต่อวงจร POS ลง Output ที่ช่องตรวจสอบสถานะ Logic เพราะเพื่อจะดูความแตกต่างของ SOP และ POS ได้ชัดเจนยิ่งขึ้น และจากโจทย์คือ เราต้องตรวจสอบ Input ทั้งสามด้วยว่า เราป้อน Input ที่เหมือนกันหรือเปล่า ถ้าเหมือนกัน ไฟ Output สีเขียวก็ติด แต่ถ้ามี input ใดที่ต่างจากเพื่อน ไฟ output จากสีเขียวก็กลายเป็นสีแดง

Digital Weekly Jurnal#2 :: NUMBER SYSTEM

Number System ระบบเลขฐาน

                ระบบเลขฐานมีไว้เพื่อช่วยในเรื่องการจัดการระบบดิจิตอลหรือระบบอิเล็กทรอนิกส์ในคอมพิวเตอร์ หรือแทนด้วยรหัสข้อมูลในระบบ BCD , EBCDIC , ASCII ซึ่งระบบเลขฐานที่สำคัญนั้นมีอยู่ด้วยกันดังนี้

           1.ระบบเลขฐาน 2  (Binary Number System) เป็นเลขฐานที่ประกอบไปด้วยตัวเลข 2 ตัวคือ 0 กับ 1 ซึ่งเป็นเลขฐานที่คอมพิวเตอร์หรืออุปกรณ์อิเล็กทรอนิกส์เข้าใจง่ายเพราะว่าสถานะทางไฟฟ้ามันบ่งบอกมาเพียง 2 สถานะคือ เปิด กับ ปิด ซึ่งเทียบได้กับ 0 กับ 1

           2. ระบบเลขฐาน 8 (Octal Number System) เป็นเลขฐานที่ประกอบไปด้วยตัวเลข 8 ตัว คือ 0 , 1 , 2 , 3 , 4 , 5 , 6 และ 7 ซึ่งเป็นเลขฐานที่เพิ่มเนื้อที่ในการเก็บข้อมูลได้มากกว่าระบบเลขฐาน 2

           3. ระบบเลขฐาน 10 (Decimal Number System) เป็นเลขฐานที่ประกอบไปด้วยตัวเลข 10 ตัว คือ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 และ 9 ซึ่งระบบเลขฐาน 10 นี้เป็นระบบเลขฐานที่คนทุกคนใช้ในชีวิตประจำวันซึ่งใช้มาตลอด สามารถจพและคำนวณได้ง่ายกว่าเลขฐานอื่นๆ

           4. ระบบเลขฐาน 16 (Hexadecimal Number System) เป็นเลขฐานที่ประกอบไปด้วยตัวเลข 10 ตัวและตัวอักษรภาษาอังกฤษอีก 6 ตัว คือ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 และตัวอักษรภาษาอังกฤษแทนตัวเลข 10 – 15 ได้แก่ A , B , C , D , E , F ซึ่งระบบเลขฐาน16นี้จะเก็บได้มากกว่าระบบเลขฐาน 2 ฐาน 8 ฐาน 10

ตารางแสดงตัวเลขระบบฐานต่างๆ

Ref :: http://www.sr.ac.th/sr_com/page_309.html

Binary Arithmetic

                การดำเนินการทางคณิตศาสตร์ของระบบเลขฐานนั้น ซึ่งในชีวิตประจำวันนั้นเราจะใช้การดำเนินการทางคณิตศาสตร์ของระบบเลขฐาน 10 ซะส่วนใหญ่ เพราะคนส่วนใหญ่จะเข้าใจง่ายและชินกับตัวเลข 0-9 ไปซะแล้ว แต่ในมุมหนึ่ง ระบบเลขฐานสองก็สามาระกระทำการทางคณิตศาสตร์ได้เหมือนกัน ซึ่งเพียงแค่แปลงตัวเลขระบบฐาน 10 ของแต่ละตัวนั้นให้กลายเป็นตัวเลขฐาน 2 ซะ และสุดท้ายที่สำคัญคือ ผลลัพธ์ที่ได้จะต้องสอดคล้องกับความเป็นจริงเช่นกัน(ระบบเลขฐาน10) เช่น

                                5  +  3  =  8

                                (0101)2 + (0011)2 = (1000)2

                สรุป Binary Arithmetic คือ การดำเนินการทางคณิตศาสตร์ของระบบเลขฐาน 2 เช่น บวก , ลบ , คูณ , หาร

การบวกเลขฐาน 2

                การบวกเลขฐาน 2 นั้นไม่ได้มีอะไรต่างจากการบวกเลขฐาน 10 เพียงแค่ตัวเลขที่ใช้มีเพียงแค่ 0 กับ 1 เท่านั้น

Truth Table

A + B	ผลลัพธ์ในระบบเลขฐาน 2	ผลลัพธ์ในระบบเลขฐาน 10
0 + 0	0	0
0 + 1	1	1
1 + 0	1	1
1 + 1	10	2
1 + 1 + 1	11	3

ตัวอย่าการบวกเลขฐาน 2

                                                                               11    1        <----- Carry  Bits ------>             11

1001101                                                 1001001                                                1000111

           + 0010010                                             +  0011001                                            + 0010110

            ---------------                                            ---------------                                            ----------------

              1011111                                                  1100010                                                1011101

Carry Bits เป็นเหมือนตัวเลขที่ทดไปยังหลักถัดไป

          จากตัวอย่างการบวกเลขฐาน 2 ทั้งสามตัวอย่างนี้ สามารถสรุปตัวอย่างได้ดังนี้

ตัวอย่างที่ 1  เป็นการบวกเลขปกติ ไม่น่าจะมีอะไรมาก

ตัวอย่างที่ 2 และตัวอย่างที่ 3 เป็นการบวกที่มีการทดตัวเลข เช่น 1+1=10 ในระบบเลขฐานสอง ซึ่งเราจะเขียนเฉพาตัวเลขที่อยู่ข้างหลังสุดเท่านั้นส่วนตัวเลขข้างหน้าก็จะทดไปให้หลักต่อไป

การลบเลขฐาน 2

Ex : 7 – 5 = 2 = 7 + (-5)

                ซึ่งการลบนั้นสามารถเขียนให้อยู่ในรูปการบวกด้วยค่าลบได้

ในเรื่องการแสดงค่าลบในเลขระบบฐาน 2 นั้น สามารถแสดงได้ในรูป Compliment

หมายเหตุ :: การ Compliment เป็นการกำหนดให้บิตซ้ายสุดมีค่าประจำหลักเป็นลบ

Ex : (1011)2 = (5)10
           (1*(-2^3))+(0*(2^2))+(1*(2^1))+(1*(2^0)) = (-5)10
                   (1*(-8))+(0*4)+(1*2)+(1*1) = (-5)10

***พึงระวังเรื่อง Data Range ไว้ด้วย***

เพิ่มเติม :: 
        MSB ( Most Significant Bit ) หรือบิตนัยสำคัญมากที่สุด คือบิตที่มีค่าประจำตำแหน่งสูงสุด โดยส่วนมากมักจะอยู่ข้างหน้าหรือทางซ้ายมือนั่นเอง

        LSB ( Least Singnificant Bit ) หรือบิตนัยสำคัญน้อยที่สุด คือบิตที่มีค่าประจำตำแหน่งต่ำสุด โดยส่วนมากมักจะอยู่ข้างหลังหรือทางขวามือนั่นเอง

        MSD ( Most Significant Digit ) หรือเลขนับสำคัญสูงสุด คือ ตัวเลขที่มีค่าประจำตำแหน่งสูงสุด ซึ่งจะอยู่ตำแหน่งขวาสุด

        LSD ( Least Significant Digit ) หรือเลขนับสำคัญต่ำสุด คือ ตัวเลขที่มีค่าประจำตำแหน่งต่ำสุด ซึ่งจะอยู่ตำแหน่งซ้ายสุด

Data Range

        Data Range คือ ช่วงข้อมูลของหน่วยความจำ มีไว้เพื่อตรวจสอบว่าข้อมูลที่ได้นั้นอยู่ในช่วงไหนขึ้นอยู่กับชนิดของการ unsigned ค่า

ตารางแสดงค่า Data Range

          2’s Compliment คืออะไร

เนื่องจากการคำนวณเลขฐานสองนั้นไม่มีการลบจึงทำการ Compliment แทน

                Ex:  00011100  ->  28

 จากตัวอย่างนี้ จะทำการ Compliment โดยมีหลักการดังนี้

  1.)  1’s Compliment เป็นการสลับเลขฐานสองให้เป็นเลขตรงข้าม เช่น แปลง 0 เป็น 1 แปลง 1 เป็น 0

                00011100  ->  11100011

  2.)  2’s Compliment เป็นวิธีต่อเนื่องจาก 1’s Compliment โดยเพิ่มเติมที่บวก 1 เข้าไป

                  11100011

                            +               1

                               11100100     -->  -28

การลบเลขฐาน 2 โดยใช้หลัก 2’s Compliment
1. ทำจำนวนหลักของตัวตั้งและตัวลบให้เท่ากัน โดยการเติม 0
2. หาค่า 2’s Compliment ของตัวลบ
3. นำค่า 2’s Compliment ของตัวลบไปบวกเข้ากับตัวตั้ง
4. เช็คจำนวนหลักของผลลัพธ์ที่ได้
 - ถ้ามีจำนวน bit ของผลลัพธ์เกินมาให้ตัดทิ้ง ผลที่ได้คือ ผลลัพธ์ของเลขฐานสางการลบกันมีค่าเป็น บวก
 - ถ้าไม่มีจำนวน bit ของผลลัพธ์เกินมาให้ทำ 2’s Compliment ผลลัพธ์อีกครั้ง ผลที่ได้คือ ผลลัพธ์ของเลขฐานสองกับการลบกันมีค่าเป็น ลบ

Ex : 7(10) - 5(10)   

                มองในรูปการบวกจะได้เป็น   7(10) + (-5(10))

    7(10) แปลงเป็นเลขฐานสองได้ 0111(2)

   -5(10) แปลงเป็นเลขฐานสองได้ 1011(2) -- > แปลงโดยใช้ 2’s Compliment.

                                                  1111    <----- Carry  Bits

                                      0111                                    

                                                +  1011                                 

                                                ---------------                                           

                                                       10010     --->  หมายเหตุ 1 เกินมา  ตัดทิ้ง                         

                Answer 0010(2)  OR  2(10)

Ex : 18 – 25

    18(10) แปลงเป็นเลขฐานสองได้ 010010(2)

    25(10) แปลงเป็นเลขฐานสองได้ 011001(2) ---> -25(10) โดย 2’s Compliment ได้ 100111(2)

                                                        11    <----- Carry  Bits

                                      100111                                               

                                                +  010110                                            

                                                ---------------                                           

                                                     111001  --- > ไม่มี bit เกินมา จะต้อง 2’s Compliment อีกครั้ง    

     2’s Compliment จะได้ 

         -   1’s Compliment  =  000110

         -   2’s Compliment  =  000110  +  1  =  000111

                   Answer  000111(2) = 7(10)

     หรืออีกวิธี ให้ MSB นั้นมีค่าประจำเป็นลบ จะได้

           (1*(-2^5))+(1*(2^4))+(1*(2^3))+(1*(2^0))) =  -7(10)

                  (1*(-32))+(1*16)+(1*8)+(1) = -7(10)

*** ควรระวังเรื่อง Binary Overflow ด้วยนะแจ๊ะ ***

 Binary Overflow

                คือการที่ผลลัพธ์กระทำเกินกว่าที่ Data Range จะรับได้

กรณีศึกษา 17+19 = 36 และ (-17)+(-19) = -36

Ex : 17(10) = 10001(2)    ::              19(10) = 10011(2)   |    -17(10) = 01111(2)       -19(10) = 01101(2)

                                         1    11         <------------ Carry  Bits ---------->         1  1111

Showing sign bits            010001                        |    showing sign bits            101111             

                                     +  010011                        |                                       +  101101

                                    ---------------                       |                                        --------------

                                         100100                        |                                          1011100  ---> 1 เกินมาตัดทิ้ง                      Answer -32 + 4 = -28  OVER FLOW         |            Answer  16 + 8 + 4 = 28  OVER FLOW

        เราต้องการคำตอบคือ 36 ในเมื่อตอนแรกนั้นเรามี bits เพียง 5 bits เท่านั้น ซึ่งเมื่อแสดงตัวเลขนั้นโดยยังไม่ต้อง 2’s Compliment นั้น จำนวนสูงสุดที่จะได้คือ (2^5) = 32 bits นั่นเอง ซึ่ง OVER FLOW 100% โดยทางแก้อันแรกเลยเพิ่มตัวเลขลงไปอีก 1 bit คือเลข 0 และ 1 (0 แทนเลขบวก,1 แทนเลขลบ) ซึ่งผลสุดท้ายจะได้ตัวเลขแบบ 6 bits ซึ่งผลที่ได้คือ (2^6) = 64 bits แต่ถ้าเป็นแบบ 2’s Compliment ล่ะก็จะแสดงได้เพียงค่า -32 ถึง 31 เท่านั้น ซึ่ง 36 มันเกิน Data Range ที่จะแสดงได้

คราวนี้เพิ่มตัวเลขเป็น 7 bits ล่ะ จะเป็นยังไง ??

กรณีศึกษา 17+19 = 36 และ (-17)+(-19) = -36

Ex : 17(10) = 10001(2)    ::         19(10) = 10011(2)   |        -17(10) = 01111(2)       -19(10) = 01101(2)

                                                1   11       <------------ Carry  Bits ---------->   11 1111              

Showing sign bits                0010001                     |    showing sign bits          1101111             

                                         +  0010011                     |                                     +  1101101

                                         ---------------                     |                                       ---------------

                                             0100100                     |                                       11011100  --->  1 เกินมาตัดทิ้ง                  Answer   0100100(2)  = 32 + 4 = +36               |            Answer  1011100(2) = - 64 + 16 + 8 + 4 = -36 

            คราวนี้ ตัวแปร 7 bits แบบ 2’s Compliment สามารถแสดงค่าได้ (2^7) = 128 นั่นคือ -64 ถึง +63 ซึ่ง 36 ไม่เกิน Data Range ที่จะแสดงได้

Detect การ OVER FLOW ??

เช็ค signed bit ของคำตอบเทียบกับ signed bit ของตัวเลขที่นำมาบวกกัน !!

-          ค่าบวก บวกกัน ผลลัพธ์ที่ได้ ต้องเป็นบวก

-          ค่าลบ บวกกัน ผลลัพธ์ที่ได้ ต้องเป็นลบ

        ที่เหนือไปกว่านั้นคือ กรณีค่าบวกกับค่าลบบวกกันจะไม่เกิด OVER FLOW !! อย่างเช่นการนำเลขค่าบวกกับค่าลบในช่วง Data Range จากตัวแปรที่มีจำนวนบิตเท่ากันมาบวกกัน ไม่ว่ายังไงผลลัพธ์จะไม่เกิน Data Range ที่แสดงแน่นอน

          แล้วจะทำวงจร Logic gate เพี่อบวกลบเลข 1 bit ได้อย่างไร ??

   Truth Table

A	B	∑	Cout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

          จาก Truth Table นี้ ถ้าเราสนใจแค่ A,B,∑ แค่นี้ล่ะก็ มันก็เหมือนกันเงื่อนไขของ OR Gate ทันทีทุกประการ ดังนั้นเราแค่ต่อ OR Gate ลงไปก็เสร็จ แต่ถ้าสนใจเรื่องของ Cout ด้วยล่ะก็ อันนี้เราก็ต่อ AND Gate เพิ่มเข้าไปด้วยนะ ซึ่ง AND Gate ให้เงื่อนไขได้ตรงกับ Truth Table ข้างต้น ซึ่งการต่อวงจรก็ศึกษาได้จากภาพดังนี้

 ซึ่งวงจรนี้เราเรียกมันว่า Half – Adder

แล้วถ้าต้องการวงจรที่บวกลบมากกว่า 1 bit หล่ะ ??

        เราก็ต่อวงจร Half – adder เพิ่มเข้าไปอีก 1 ชุด โดยที่ขา A ของ OR Gate ตัวที่ 2 นั้นก็คือผลลัพธ์จาก Half – adder ชุดที่ 1 1 ส่วนขา B ของ  OR Gate ตัวที่ 2 นั้นก็ต่อ Cin ไว้ ซึ่งวงจรที่ได้นี้เรียกว่า Full adder

Truth Table

A	B	Carry-in	Sum	Carry – out
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

วงจรบวกเลขหลายบิต 

         ก็คือการต่อวงจร Full adder ต่อเรียงกันตามจำนวนบิต โดย Cin เริ่มต้นนั้นต้องต่อ GND ไว้เสมือนแทนเลข 0 ลงไป

วงจรลบเลข

         เราก็ใช้หลักของ 2’s Compliment ในการทำวงจร โดยการต่อวงจร Full Adder เหมือนเดิม เพิ่มเติมที่มี XOR ใช้ในการสลับตัวเลข และคราวนี้ในส่วนของ Cin นั้น เราก็ต่อไปที่ live switch เพื่อเลื่อนค่า โดยที่  ( 0 = ค่าบวก , 1 = ค่าลบ )

การตรวจจับ OVER FLOW

           วงจรตรวจจับ OVER FLOW สามารถทำได้อย่างง่ายได้ เพียงแค่ต่อ XOR ระหว่า cin กับ cout ที่ MSB ( Most Significant Bit )